Math Competitions
This is an
annual competition held at your high school every March or April. In 2001-2002,
it was held on March 26 and April 9. It is open for students who perform well
on the American Mathematics Contest 10 or the American Mathematics Contest 12.
It contains 15 challenging questions with answers being integers from 0 to 999.
3 hours are given for this contest. More information can be found here.
Sample Problem
What is the largest 2-digit prime factor of 
?
This is an
annual competition held at your high school every February. It is open for any
student in grade 10 or below. In 2001-2002, it was held on February 12 and February 27.
It contains 25 multiple choice questions. 75 minutes are given for this contest. More information can be found here.
Sample Problem
What is the maximum number for the possible
points of intersection of a circle and a triangle?
This is an annual
competition held at your high school every February. In 2001-2002, it was
held on February 12 and February 27. It contains 25 multiple choice
questions. 75 minutes are given for this contest. More information can be found here.
Sample Problem
Let f be a function
satisfying 
for
all positive real numbers x and y. If 
,
what is the value of 
?
American Regions Math League
This is an annual
competition held simultaneously at San Jose State University, University of
Iowa, and Penn State every June. It contains an individual round, with 8
questions, 10 minutes per pair. There is also a relay round, a team round, and a
power (proof) round. In 2001-2002, it will be held on May 31 and
June 1. More information can be found here.
Sample Problem
The measure of the vertex
angle of isosceles triangle ABC is 
and the sides of the triangle are 
, 
,
and .
Compute the area of 
.
Bay Area Math Meet
This is an annual competition held at University
of San Francisco every April. More information can be found here.
Sample Problem
Find the probability that a number from the set 
is divisible by 7 or 11 (or both).
Bay Area Math Olympiad
This is a
competition held annually at your high school every February. In 2001-2002, it
will be held on February 26. More information can be found here.
Sample Problem
Let JHIZ be a rectangle, and let A and C be points on sides ZI and ZJ, respectively. The perpendicular from A to CH intersects line HI at X, and the perpendicular from C to AH intersects line HJ at Y. Prove that X, Y and Z are collinear (lie on the same line).
California Math League
This is a competition held
six times per year at your high school. There is one in October, one in
November, one in December, one in January, one in February, and one in March.
In 2001-2002, they will be held on October 30, December 4, January 8, February
5, March 5, and April 9. More information can be found here.
Sample Problem
If i represents the imaginary unit, what
is the ordered pair of real numbers (a, b) for which 
?
Department of Energy Math Competition
This is an annual competition held at the
Lawrence Livermore Labs every May. More information can be found here.
Sample Problem
What two integers, neither containing any zeros, when multiplied together, will give exactly 1,000,000,000?
Hokubei Mainichi Math Competition
This competition is held
annually in January at Santa Teresa High School. There is a Junior division for
students in grades 7-9 and a Senior division for students in grades 10-12.
Sample Problem
Coming soon hopefully
This competition is held annually
in July, in a different country each year. A country can send six students to
the International Mathematical Olympiad each year. In the United States, these
people will are among the top twelve students in the USA Mathematical Olympiad.
More information can be found here.
Sample Problem
Let a, b, c,
d be integers with 
.
Suppose that 
.
Prove that 
is not prime.
This competition is held
four times per year at your high school. The dates are in November, January,
February, and March. In 2001-2002, they will be held on October 22, November
26, January 21, and February 25. More information can be found here.
Sample Problem
A quadrilateral inscribed in a circle has side lengths 17, 99, 19, and 97. Find the area of the circle.
Polya
This is an annual
competition held at Castilleja School every October or November. In 2001-2002,
it will be held on November 17. More information can be found here.
Sample Problem
Find all integers n > 3 such that n – 3
divides evenly into 
.
College of Creative Studies Math Competition
This is an annual competition
held annually at your high school. The first round is a preliminary round held
in October. For students who perform well on this preliminary round, there is
an advanced round held in November.
Sample Problem
Preliminary round: An equilateral triangle is inscribed in a circle of radius 2 inches. What is the area of the triangle?
Advanced round: A number is said to be rational
if it can be expressed as the ratio of two integers. Prove that the tangent of 
degrees is not
rational.
Santa Clara High School Math Contest
This is an annual competition held at Santa Clara
University every November. More information can be found here.
Sample Problem
In how many
ways can the numbers 1, 2, 3, 4, 5, 6 be arranged as a sequence u, v, w, x, y,
z such that u + x = v + y = w + z?
Santa Clara Valley Math Field Day
This is an annual
competition held at San Jose State University every March. In 2001-2002, it
will be held on March 23. There are seven divisions for competition: Algebra I,
Geometry, Algebra II, Open (Trigonometry and Precalculus), Calculus, Leapfrog,
and Discovery Quest. For the first five of these, you must be currently
enrolled in a class covering those topics to enter.
Sample Problem
Algebra I: Find the domain of the following
equation: 
.
Geometry: A square and an equilateral triangle have equal perimeters. The area of the triangle is 93 square inches. Expressed in inches what is the diagonal of the square?
Algebra II: Simplify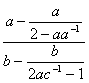 
.
Open: What is the center of an ellipse whose
equation is 
?
Calculus: What is the value of 
?
Leap Frog: What is the smallest natural number with exactly 24 divisors?
Discovery Quest: Hopefully coming soon
This is an annual competition held at Stanford
University every February. More information can be found here.
Sample Problem
Advanced Topics: Evaluate 
.
Algebra: Find all solutions to 
.
Calculus: Let 
. If 
, then find 
.
Geometry: In a triangle the
sum of squares of medians is 96. What is the maximum possible value of the sum
of the medians?
General: How many permutations of 123456 have
exactly one number in the correct place?
This is an annual competition
which is held in Massachusetts in May each year. In 2001-2002, it will be held
on May 2-5. It is open to all students who perform well on the American
Invitational Mathematics Examination. More information can be found here.
Sample Problem
Prove that the average of the numbers 
is cot 1°.
USA Mathematical Talent Search
This contest is held four times
per year. You get the questions with about a month to solve them, using
whatever references you want, as long as those references are not other people.
Due dates are in October, November, January, and March. In 2001-2002, these due
dates are October 8, November 25, January 6, and March 17. More information can
be found here.
Sample Problem
We define the repetition
number of a positive integer n to be the number of distinct digits
of n when written in base 10. Prove that each integer has a multiple
which has a repetition number less than or equal to 2.