Write out some terms
.
Multiply by r
.
Subtract
.
Divide by r – 1.
.
We decompose the series into a bunch of
geometric series.
.
We know how to sum all these geometric series, so we get
.
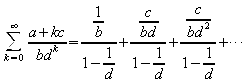That can also be summed more nicely, reaching
,
which, with a little algebra, gives
We use a partial fraction decomposition.
. Now we must solve for A and B. So, we cross-multiply to get
. By letting k equal –1 or 0, we can solve and get A = 1 and B =
-1. Thus we get
.
Writing a few terms shows the answer quickly:
because
the terms cancel.
Proof
We create a
polynomial
.
Using Taylor series, we see that
.
If we are looking for the roots of P(x)=0, then sin x
must equal 0, so
.
Therefore, we can factor P(x) based on its roots into
.
So, multiplying the successive terms,
.
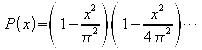Now we can expand this polynomial to get
,
where all we need to know is the x^2 coefficient. Then we have
,
and after some multiplication, .
5) Alternating Harmonic Series
Proof
Calculus
students may remember that the Taylor series for
is
.
Letting
x = 1 in this taylor polynomial, we get the
desired summation,
.
6) Reciprocal Factorials
Proof
First, we recall the
definition
.
Now we can begin to expand this using the binomial theorem. We get
.
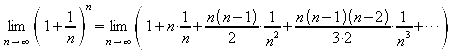Ridding ourselves of the terms that vanish, we get
.
7) Arithmetic/Reciprocal Factorials
Proof
We rewrite this as
two summations:
.
Manipulation of the first factorial gives
.
The other term goes to e. However, this other term is equivalent, so
we get
.