Theorems
Pythagorean Theorem
In a right triangle, the sum of the squares of the legs is equal to the square of the hypotenuse.

Proof
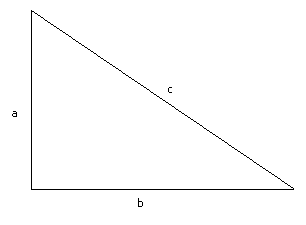
We create a square with side length![]() .
Within that square, we create four right triangles with legs a and b
and hypotenuse c. Thus we get a square with side length c in the
center. Now we perform some algebra. The area of the big square is
.
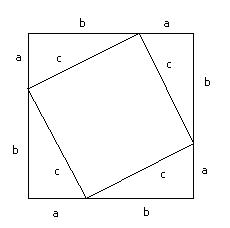
Within that square, we create four right triangles with legs a and b
and hypotenuse c. Thus we get a square with side length c in the
center. Now we perform some algebra. The area of the big square is![]() .
The area of each small triangle is
.
The area of each small triangle is![]() .
Thus the area of all four triangles is
.
Thus the area of all four triangles is
![]() .
Subtracting, we get the area of the center square to be
.
Subtracting, we get the area of the center square to be![]() . However, the side of the square is of length c, so its area is
. However, the side of the square is of length c, so its area is![]() .
Thus
.
Thus![]() .
.
There is no way to write
![]() as the ratio of two integers.
as the ratio of two integers.
We will work by contradiction. Assume that there is a fraction
![]() ,
and that this fraction is in its simplest form. Squaring that, we
get
,
and that this fraction is in its simplest form. Squaring that, we
get
![]() ,
or
,
or
![]() .
Therefore,
.
Therefore,
![]() must
be even, so p must be even. Then
must
be even, so p must be even. Then
![]() must
be divisible by 4. So
must
be divisible by 4. So
![]() is
even. But if
is
even. But if
![]() and
and
![]() ,
and thus also p and q, are even, then this fraction is not in
simplest form, as we can simply divide numerator and denominator by
2. Thus we have reached a contradiction, and
,
and thus also p and q, are even, then this fraction is not in
simplest form, as we can simply divide numerator and denominator by
2. Thus we have reached a contradiction, and
![]() is
irrational.
is
irrational.
There are an infinite number of primes
Assume that there are a finite number of primes. Then we will have a largest prime. Then we can multiply all the primes together to get a number m. Then we will add one. Since all primes are factors of the large product, m-1, none can be factors of m. Thus this new number will be a prime, and so we have reached a contradiction, and there are infinitely many primes.
Law of Sines
In any triangle
![]() ,
where R is the circumradius.
,
where R is the circumradius.
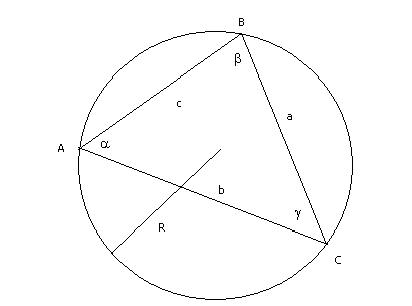
Proof
First we prove this
without the 2R term. Drop an altitude h from vertex A to BC, so it
intersects at D. Because of the two triangles,
![]() .
If we drop altitude f from vertex B to AC, we get something similar,
namely
.
If we drop altitude f from vertex B to AC, we get something similar,
namely
![]() .
Some multiplication and division yields
.
Some multiplication and division yields
![]() .
Now we need a new picture to prove the 2R part:
.
Now we need a new picture to prove the 2R part:
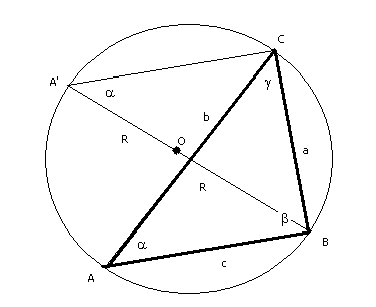
The original triangle is
now in bold lines. We created A' such that
![]() will be 90°. Also
will be 90°. Also
![]() .
Therefore, we have
.
Therefore, we have
![]() .
And thus we are done.
.
And thus we are done.
Law of Cosines
In any triangle
![]() .
.
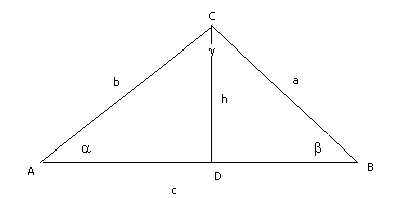
Proof
In the diagram
above,
![]() ,
and
,
and
![]() .
By the Pythagorean Theorem,
.
By the Pythagorean Theorem,
![]() .
Then
.
Then
![]() .
Also
.
Also
![]() .
Thus
.
Thus
![]() .
.
The area of a triangle is equal to
![]() ,
where a, b, and c are the side lengths and
,
where a, b, and c are the side lengths and
![]() .
.
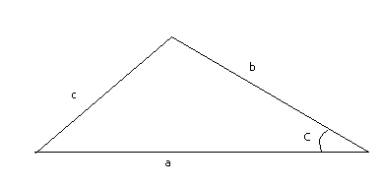
Let K be the area of the triangle. We know that the area of a
triangle is equal to
![]() ,
where a and b are sides and C is the angle between them. Therefore,
.
,
where a and b are sides and C is the angle between them. Therefore,
.
![]() Applying
the law of cosines yields
Applying
the law of cosines yields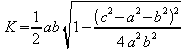 . Applying a bit of algebra gives
. Applying a bit of algebra gives
![]() ,
or, after factoring,
,
or, after factoring,![]() .
This yields
.
This yields
![]() .
Now we finally introduce s, giving
.
Now we finally introduce s, giving
![]() .
.
In the triangle below,![]() .
.
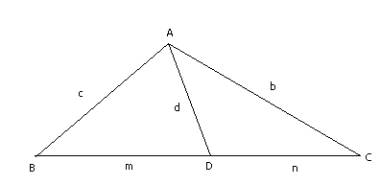
We use the law of cosines:![]() , so
, so![]() . Also, m + n = a, so we get
. Also, m + n = a, so we get
![]() ,
and we are done.
,
and we are done.
In a cyclic quadrilateral,
![]() .
.
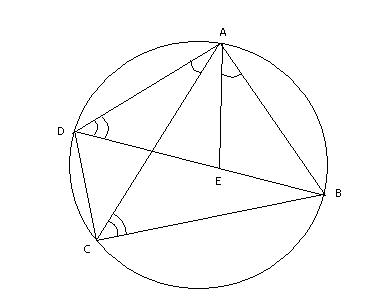
![]() .
Therefore we can choose a point E on DB such that
.
Therefore we can choose a point E on DB such that![]() , thus guaranteeing
, thus guaranteeing![]() .
Manipulating equal angles yields
.
Manipulating equal angles yields
![]() ,
so
,
so![]() and
and![]() . Cross-multiplying and adding yields
. Cross-multiplying and adding yields![]() , so we are done.
, so we are done.
![]()
We can write
![]() .
Then, for each number k of x’s in the summation, you can get
that number by choosing k x’s from the n terms. The number of
ways to choose those k x’s is
.
Then, for each number k of x’s in the summation, you can get
that number by choosing k x’s from the n terms. The number of
ways to choose those k x’s is![]() . Summing over all the possible number of x’s, we reach the
summation
. Summing over all the possible number of x’s, we reach the
summation
![]() .
.
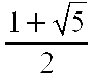
We let
![]() .
Since
.
Since
![]() ,
we may rewrite this as
,
we may rewrite this as![]() . Since we are taking a limit as n goes to infinity, the ratio must
remain constant between successive terms. Thus we get
. Since we are taking a limit as n goes to infinity, the ratio must
remain constant between successive terms. Thus we get![]() .
Solving this equation shows that
.
Solving this equation shows that
![]() ,
which is the famous golden ratio.
,
which is the famous golden ratio.
In the triangle below, ![]() if
X, Y, and Z are collinear.
if
X, Y, and Z are collinear.
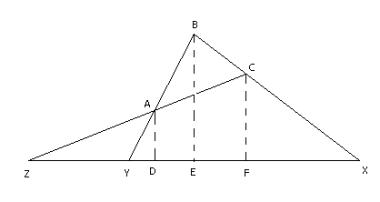
We have three sets of similar triangles:![]() ,
,![]() , and
, and![]() . Therefore, we have
. Therefore, we have![]() ,
,![]() , and
, and![]() . When we multiply all the left hand sides of all three equalities,
then multiply all the right hand sides, we get
. When we multiply all the left hand sides of all three equalities,
then multiply all the right hand sides, we get
![]() .
.
If three cevians of a triangle, one from each vertex, are
concurrent, then
![]() .
.
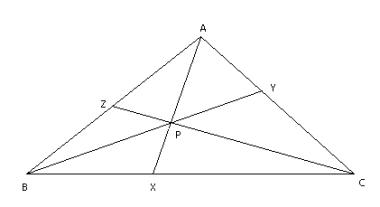
I will use the notation
![]() to
denote the area of triangle ABC. By proportions,
to
denote the area of triangle ABC. By proportions,![]() . Also,
. Also,![]() and
and![]() .
Multiplying these three equations gives
.
Multiplying these three equations gives
![]() .
.
![]() if
p is prime.
if
p is prime.
Since p is prime, we can find a primitive root![]() .
By the definition of a primitive root
.
By the definition of a primitive root![]() . Then
. Then![]() . Also
. Also![]() by
Fermat's Little Theorem
, so
by
Fermat's Little Theorem
, so![]() . Letting
. Letting![]() , we get
, we get
![]() ,
so
,
so
![]() .
Because a is a primitive root,
.
Because a is a primitive root,
![]() .
Thus
.
Thus
![]() ,
and we are done.
,
and we are done.
Countability of Rational Numbers
There are the same number of rational numbers as there are integers
Proof
If we can find some way of pairing off all the rational numbers with all the integers, then there must be the same number of each. Here is Georg Cantor's brilliant demonstration of this:

Using
this diagonalization method, Cantor found a way to pair every
rational number with a real number. Thus they have the same number.
(Thanks to my friend Timothy Nguyen for this picture.)
Uncountability of the Real Numbers
There are more real numbers than integers.
Proof
Let us write out all of the real numbers in decimal form. If we write them in random order, we will get a list like this one:

Now we shall choose the
first decimal of the first number, the second decimal of the second
number, the third decimal of the third number, and so on, to get a
number like this:
![]() .
Now we change each digit of this number to get a number like this:
.
Now we change each digit of this number to get a number like this:
![]() .
According to the proviso that the list contains all real numbers,
this number must be somewhere on this list. But this is not possible!
We have changed every digit of the diagonal number, so this new
number cannot be the first, or the second, or the third, or any of
the numbers in the list. Therefore the real numbers cannot be paired
off with the integers. Thus there are more real numbers than
integers.
.
According to the proviso that the list contains all real numbers,
this number must be somewhere on this list. But this is not possible!
We have changed every digit of the diagonal number, so this new
number cannot be the first, or the second, or the third, or any of
the numbers in the list. Therefore the real numbers cannot be paired
off with the integers. Thus there are more real numbers than
integers.
Divergence of the Harmonic Series
The harmonic series,
![]() ,
divergees to infinity.
,
divergees to infinity.
Proof
Suppose this series
converges to a sum S. Thus we have
![]() .
Obviously
.
Obviously
![]() .
Combining consecutive terms in this inequality, we get
.
Combining consecutive terms in this inequality, we get
![]() .
But now we have reached a contradiction, as
.
But now we have reached a contradiction, as
![]() .
Therefore S diverges to infinity.
.
Therefore S diverges to infinity.
DeMoivre's Theorem
If
![]() is
a complex number, then we can write it in the form
is
a complex number, then we can write it in the form
![]() .
Then
.
Then
![]() .
.
Proof
![]() ,
as Euler demonstrated. Thus changing the form of
,
as Euler demonstrated. Thus changing the form of
![]() ,
we easily get
,
we easily get
![]() .
.
Fundamental Theorem of Arithmetic
Every positive integer other than one can be written as the product of primes in exactly one way.
Proof
Because of the definition
of a prime, we know that all positive integers other than one can be
written as the product of primes in at least one way. So we work by
contradiction. Let N be the smallest number that is the product of
primes in two or more different ways. Thus
![]() ,
where all the ps and qs are primes which are not necessarily
distinct. Therefore
,
where all the ps and qs are primes which are not necessarily
distinct. Therefore
![]() .
Thus it divides one of the qs since they are primes. Without loss of
generality, therefore,
.
Thus it divides one of the qs since they are primes. Without loss of
generality, therefore,
![]() .
So
.
So
![]() .
Then
.
Then
![]() .
Thus
.
Thus
![]() is a number smaller than N which can also be written as the product
of primes in at least two different ways. Therefore, we have reached
a contradiction, so we are done.
is a number smaller than N which can also be written as the product
of primes in at least two different ways. Therefore, we have reached
a contradiction, so we are done.